On June 10, a research paper Nonparametric Power-law Surrogates by Professor YAN Gang’s team from the School of Physics Science and Engineering of Tongji University, and Frontiers Science Center for Intelligent Autonomous Systems was published in Physical Review X. In this paper, a new and theoretically supported nonparametric approach is proposed to expand the effectiveness and applicability of a power-law model in small samples and noisy data, providing an insight into revealing the underlying mechanism of real complex systems.
Heavy-tailed distribution is a distribution whose tail decay rate is slower than index. This kind of distribution widely appears in physical, biological, economic, and social complex systems. Heavy-tailed distribution means that the probability of extreme events is much greater than what people usually think, that is, events may suddenly take on an unprecedented scale. In this distribution, power-law distribution is particularly important, because it can not only reveal interesting new phenomena (such as the scale-free characteristics of real networks, and the phase transition behavior of physical systems), but also often contain anti-intuitive underlying mechanisms (such as the critical state of brain activity, and the self-organized criticality of natural clusters). The sample size of actual observation data (especially extreme events) is often very small, limited by the finite scale effect, and contains a variety of noises. Therefore, judging whether a real system is in a critical state (that is, whether its activities obey the power-law distribution) is an important scientific problem which has become a hot issue and triggered debate in the academic community in recent years.
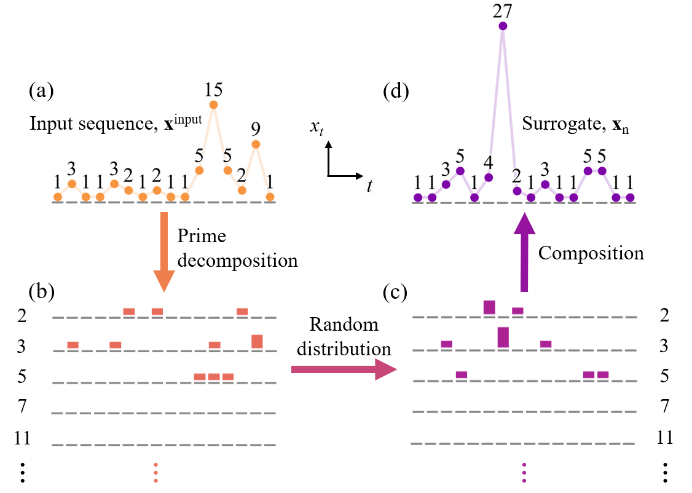
Figure 1: Schematic diagram of power-law surrogate method under constraints
At present, the commonly used power-law distribution has two important defects, which greatly limit its applicability in real systems. First, this approach can only be used in a single specific model obtained by maximum simulation, but cannot be applied to a more general power-law model. Secondly, this distribution usually assumes independent and identically distributed events, ignoring the temporal correlations of actual complex systems. In this paper, the author proposes a nonparametric surrogate method (see Figure 1), and theoretically proves the effectiveness of this method. The research results show that the new method can not only overcome the above two shortcomings of the current commonly used methods, but also significantly improve the robustness of power-law model inference (see Figure 2). This study provides a new inference method for the criticality of real complex systems, and also provides a new analysis tool for the prediction and management of extreme risks.
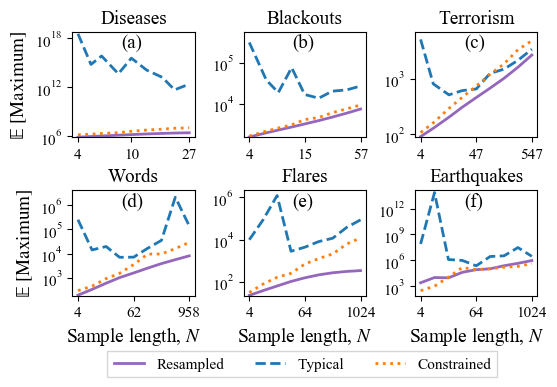
Figure 2: When the power-law model is applied to six real event sequence data, the new method proposed in this paper can estimate the scale of extreme events more accurately.
Legends: Real observation data (purple solid line),
traditional method (blue dotted line),
and the method proposed in this paper (orange dotted line).
The first author of this paper is Jack Murdoch Moore, a postdoctoral research fellow of Tongji University, and the corresponding author is Professor YAN Gang. Professor Eduardo g. Altmann of the University of Sydney also made important contributions to this study. The research was supported by the National Natural Science Foundation of China and Shanghai Municipal Science and technology major projects.
Link to paper:https://doi.org/10.1103/PhysRevX.12.021056